1次関数 傾き 求め方 285283-1次関数 傾き 切片 求め方
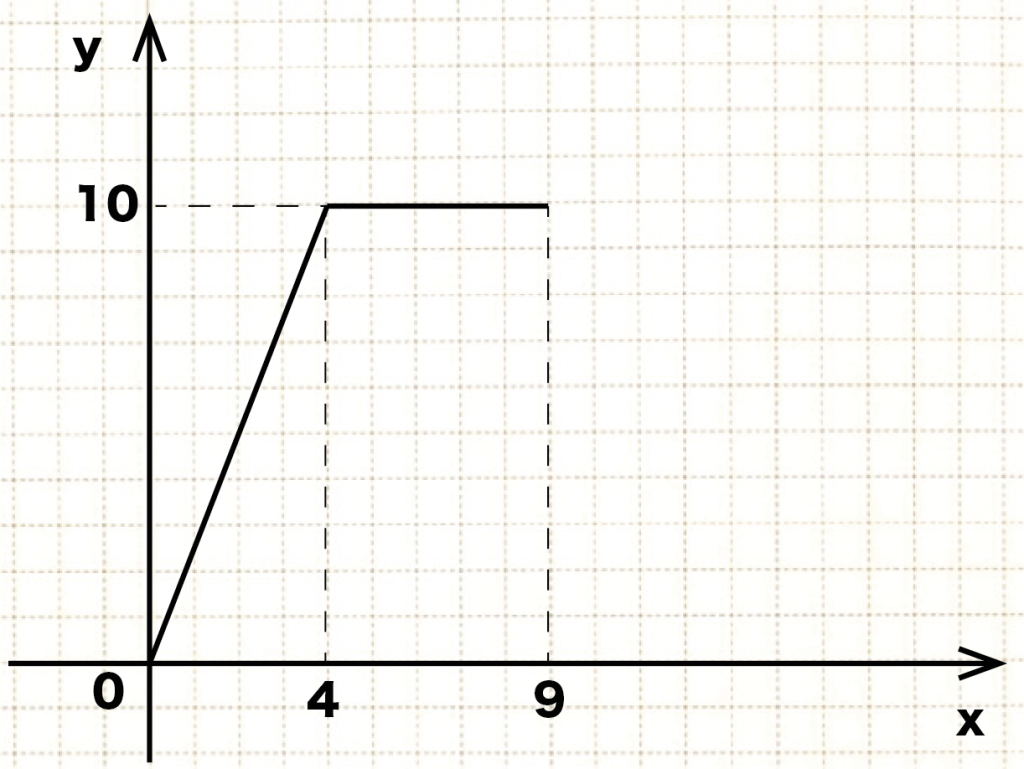
一次関数の傾きの求め方・\(3\)パターン 「一次関数の傾きの求め方が知りたい」 テストによくでる一次関数の傾きの求め方・\(3\)パターンです。 一次関数の傾きの求め方・\(3\)パターン \(1\)
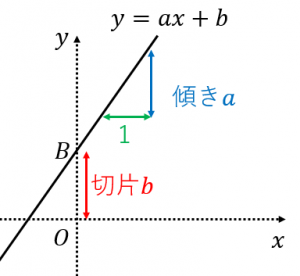
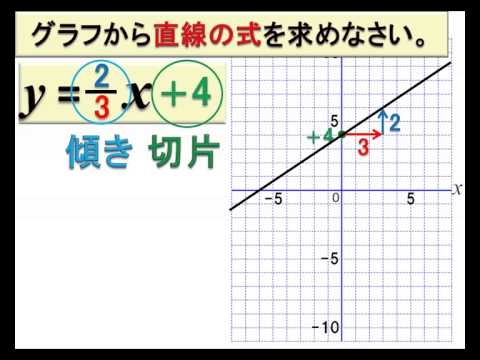
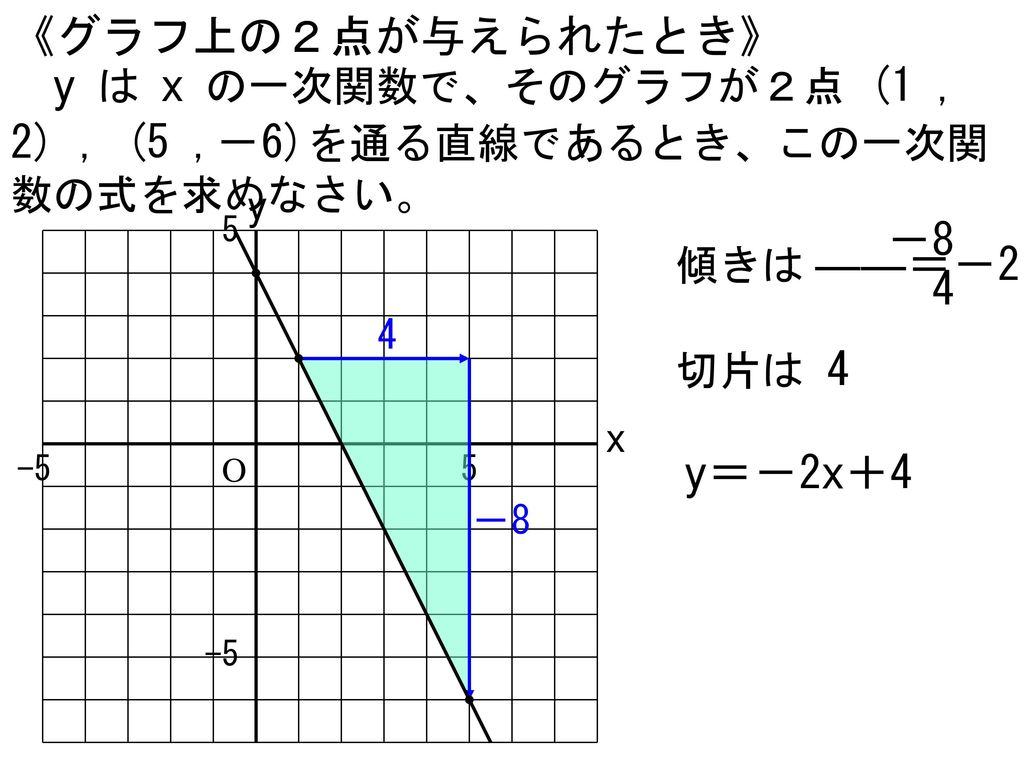
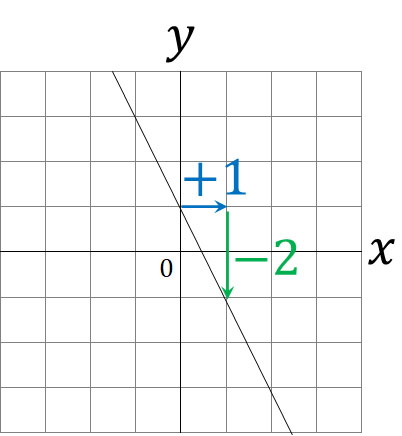
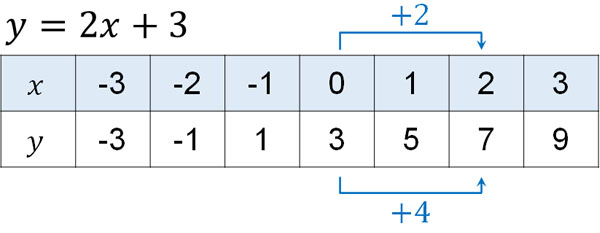
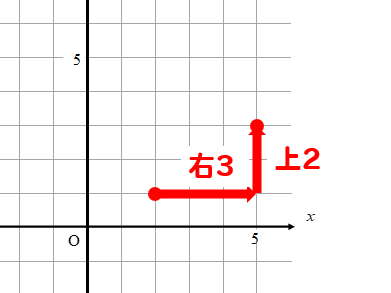
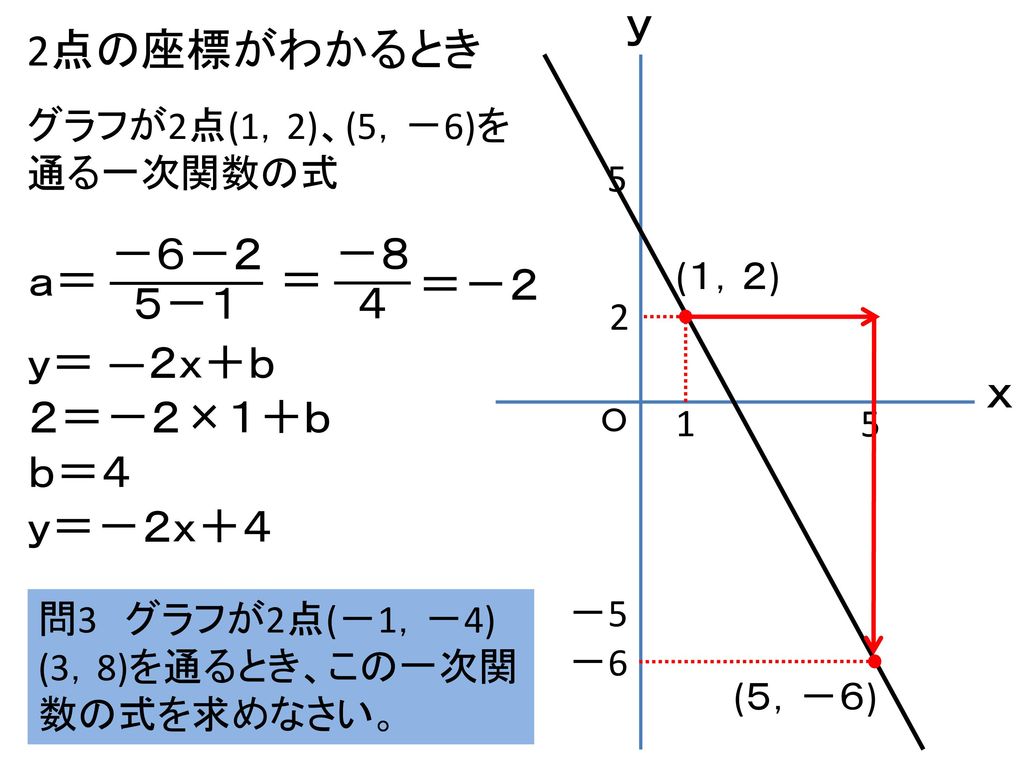
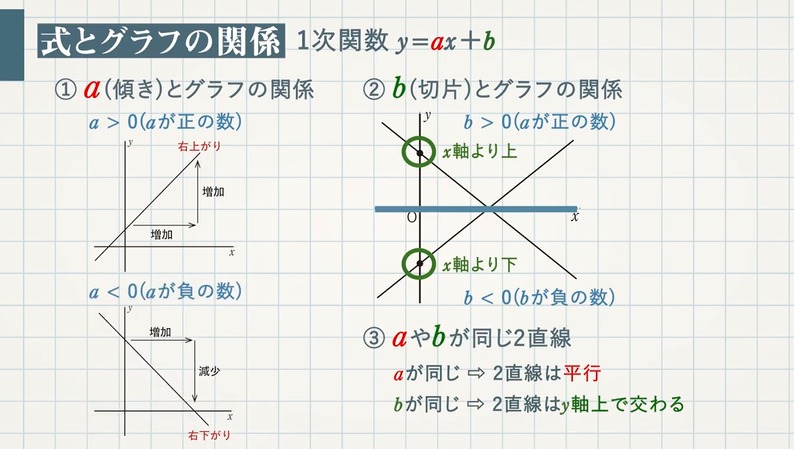
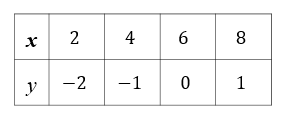
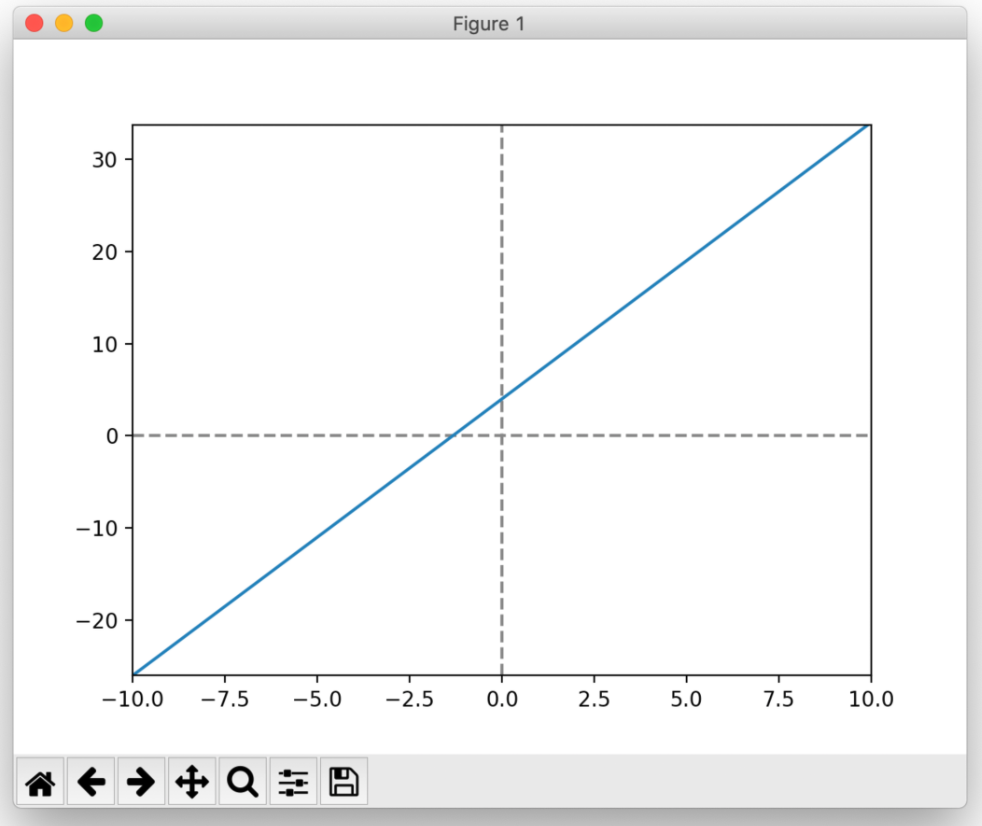
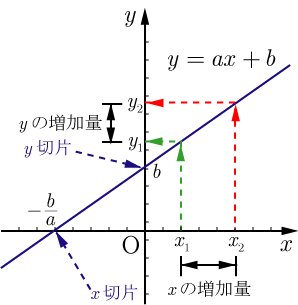
1次関数 傾き 切片 求め方-1次関数の式の求め方 (1)基本的な考え方 ※求める1次関数の式を「y=ax+b」とおいて、与えられた条件をこれに当てはめていく ①傾きと通る1点が与えられている場合 例)傾き3,点(2,4)をその他の傾きの表し方も見てみましょう。 傾きを求める公式は y 2 − y 1 x 2 − x 1 {\displaystyle {\frac {y_{2}y_{1}}{x_{2}x_{1}}}} です。 これは変化量を意味するギリシャ文字「Δ(デルタ)」を用いて
1次関数 傾き 切片 求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
 |  | |
「1次関数 傾き 切片 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | 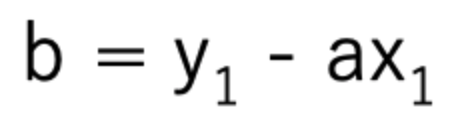 | |
 |  |  |
「1次関数 傾き 切片 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 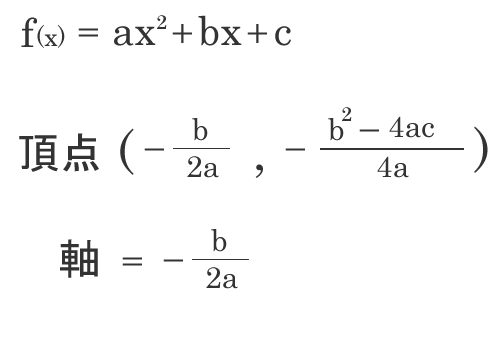 |  |
 | ||
 | 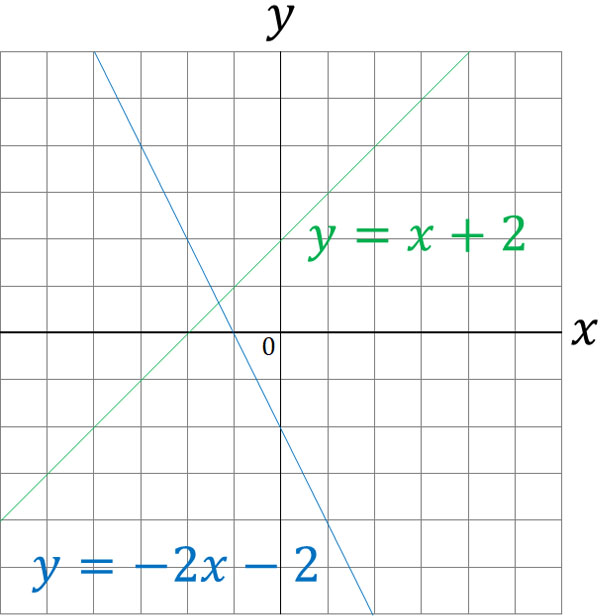 | |
 |  | |
「1次関数 傾き 切片 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
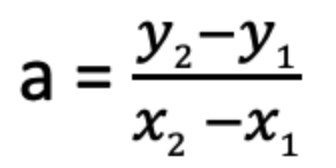 |  | |
 |  |  |
「1次関数 傾き 切片 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
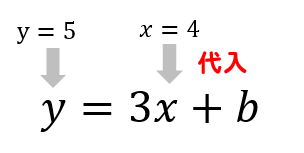 |  | |
 |  | |
 |  |  |
「1次関数 傾き 切片 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「1次関数 傾き 切片 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
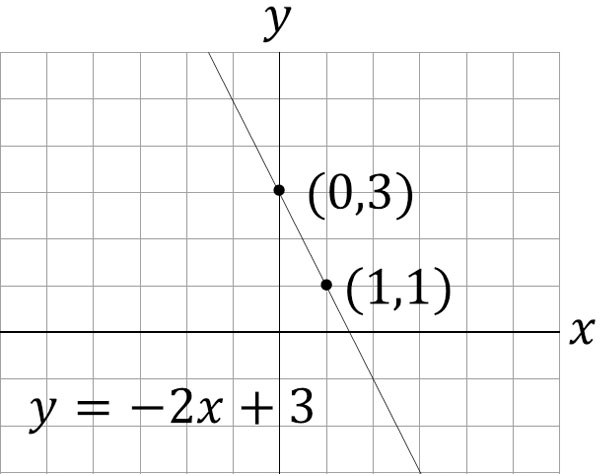 |  | |
 |  | |
「1次関数 傾き 切片 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「1次関数 傾き 切片 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
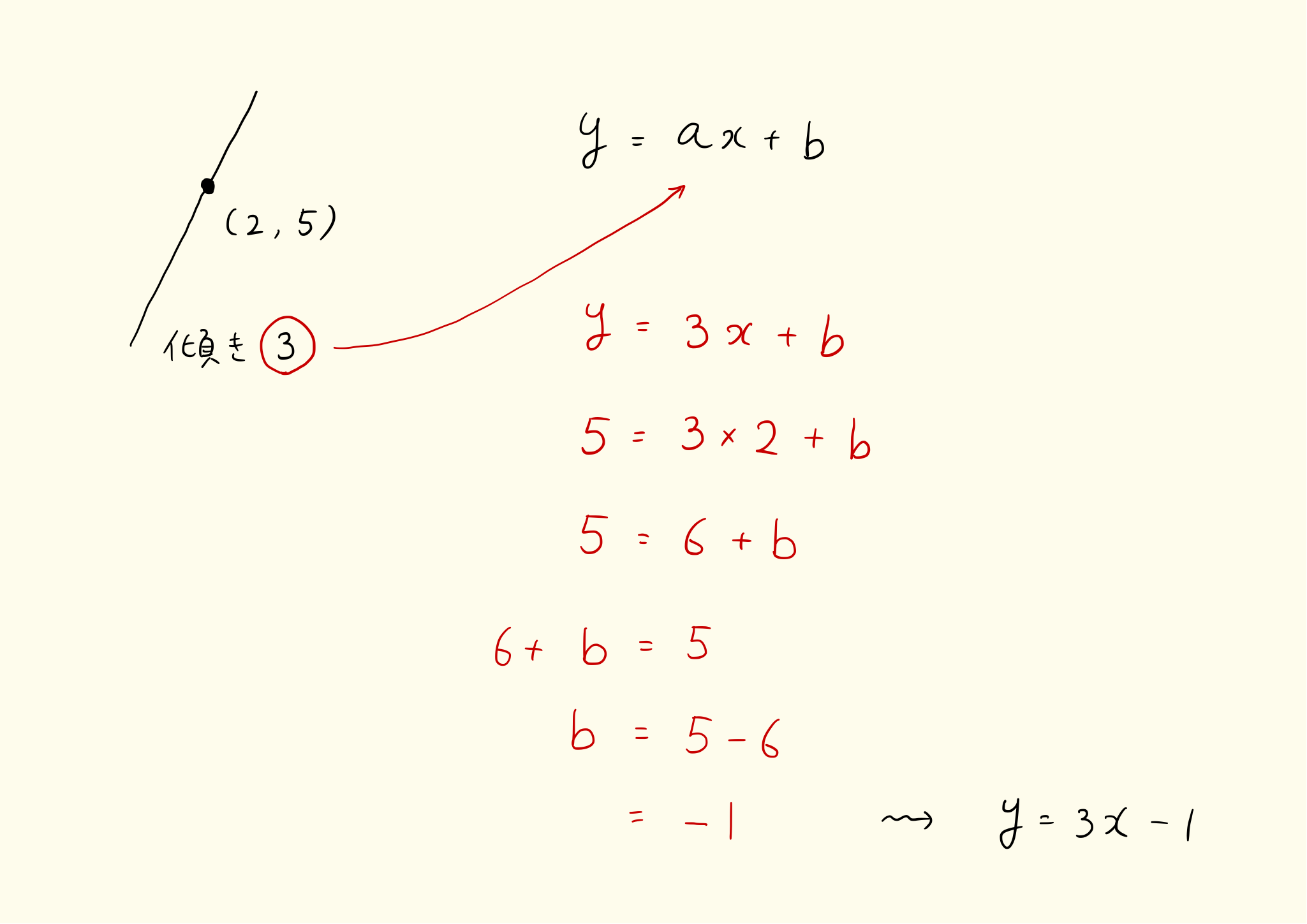 |  | |
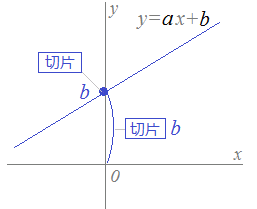 | 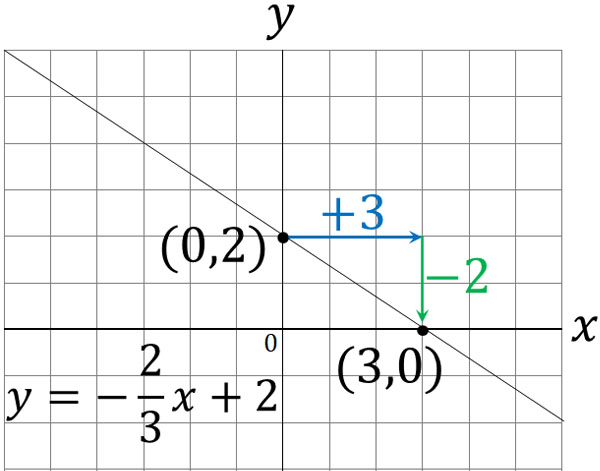 |
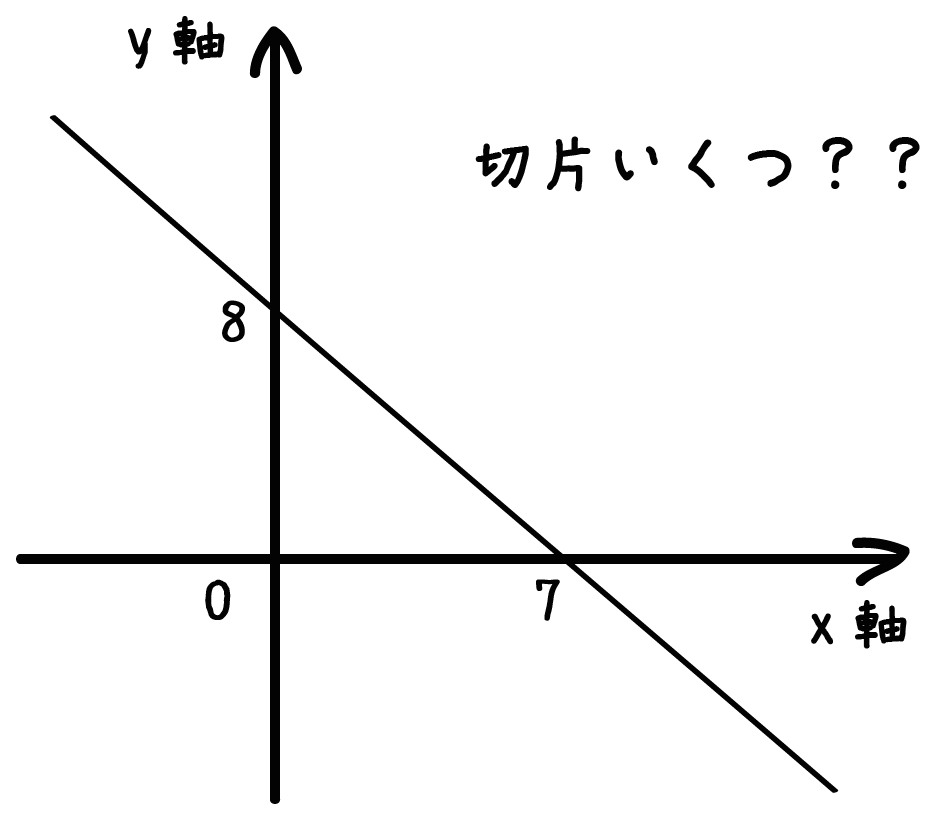
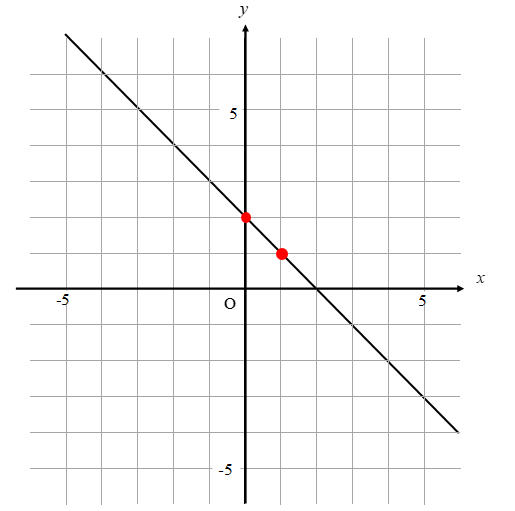
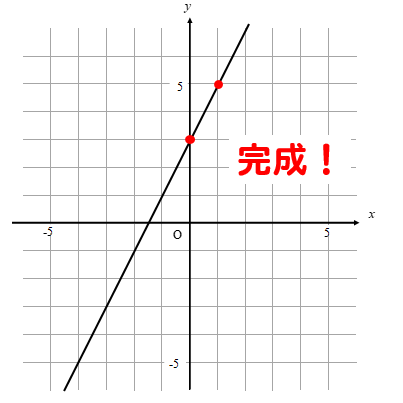
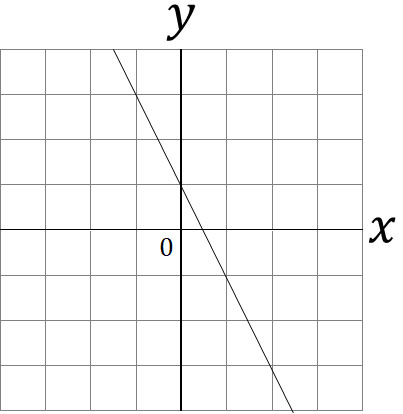
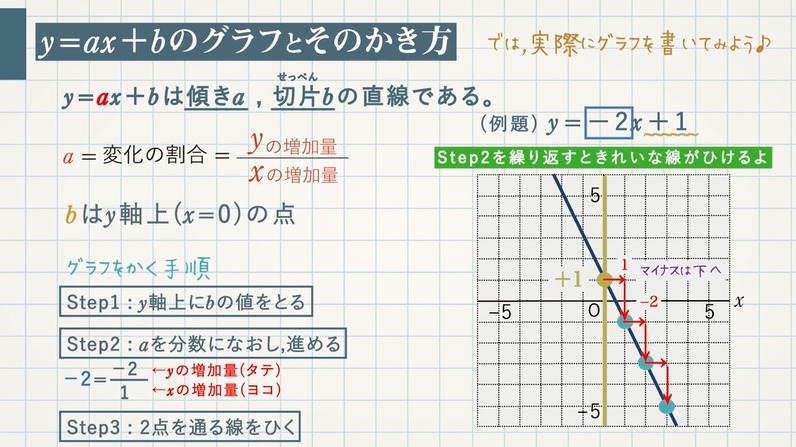
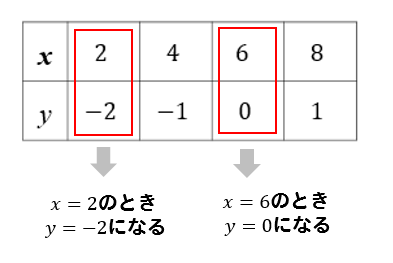
1次関数の式の出し方は大きく分けて 2通り 。 ・傾きと1点から出す方法。 ・2点から出す方法。 傾きと1点から1次関数の式を出す y = axb の傾きaとx, yに数字を代入してbを求める。 例傾き31次関数 y = ax b において、a を傾きと呼ぶのに対して、b を y切片と呼ぶ。1次関数の y切片は、グラフ(直線)が y 軸と交わる点の y 座標に等しい。したがって、y = ax b の形の方程式を「傾
Incoming Term: 1次関数 傾き 求め方, 1次関数 傾き 切片 求め方,
コメント
コメントを投稿